Thymeleaf is a popular server-side template engine for Java-based web and standalone environments. In this article, you'll learn how to use enum constant values in Thymeleaf templates.
We'll first look at how to display all enum values in a drop-down list and then how to compare enum constants in Thymeleaf. Let us say we have the following enum class named Topic.java that represents several blog topics:
Topic.java
package com.attacomsian.runner.domains.constants;
public enum Topic {
TECH,
DESIGN,
STARTUP,
WEB,
DEVTOOLS;
}
We have another model class called Post.java that stores a reference to the enum class to present the post topic:
Post.java
package com.attacomsian.runner.domains;
import com.attacomsian.runner.domains.constants.Topic;
import java.io.Serializable;
public class Post implements Serializable {
private int id;
private String title;
private String body;
private Topic topic;
// constructor, getters, and setters removed for brevity
}
Finally, we have the following controller method that handles all GET requests at the / endpoint and returns a new Post object stored in Model:
@GetMapping("/")
public String homePage(Model model) {
// add a new post object
model.addAttribute("post", new Post());
return "index";
}
How to display all enum constants
Let us now create an index.html Thymeleaf template in the src/main/resources/templates/ folder that renders an HTML form to allow users to create a new post as shown below:
index.html
<!DOCTYPE html>
<html lang="en" xmlns:th="http://www.thymeleaf.org">
<head>
<meta charset="UTF-8">
<title>Spring Boot Enum Example</title>
<link rel="stylesheet" href="https://stackpath.bootstrapcdn.com/bootstrap/4.3.1/css/bootstrap.min.css">
</head>
<body>
<div class="container my-5">
<div class="row">
<div class="col-8 mx-auto">
<h1>Create New Post</h1>
<form th:action="@{/save-post}" th:object="${post}" method="post">
<div class="form-row">
<div class="col-md-6">
<div class="form-group">
<label for="title">Title</label>
<input type="text" id="title" th:field="*{title}" class="form-control">
</div>
</div>
<div class="col-md-6">
<div class="form-group">
<label for="topic">Select Topic</label>
<select class="form-control" id="topic" th:field="*{topic}">
<option th:each="topic : ${T(com.attacomsian.runner.domains.constants.Topic).values()}"
th:value="${topic}" th:text="${topic}"></option>
</select>
</div>
</div>
</div>
<div class="form-group">
<label for="body">Body</label>
<textarea id="body" th:field="*{body}" class="form-control"></textarea>
</div>
<button type="submit" class="btn btn-primary btn-block">Submit</button>
</form>
</div>
</div>
</div>
</body>
</html>
As you can see above, we are generating a drop-down list with all topics available to select. The Topic enum class provides the values() method that returns all enum constants as an array.
The T operator is a part of SpEL (Spring Expression Language) for accessing a type and invoking static methods or getting static properties. We used it for accessing all the values from our enum class Topic.
Now, if you run the application, you will see the following HTML form rendered in the browser:
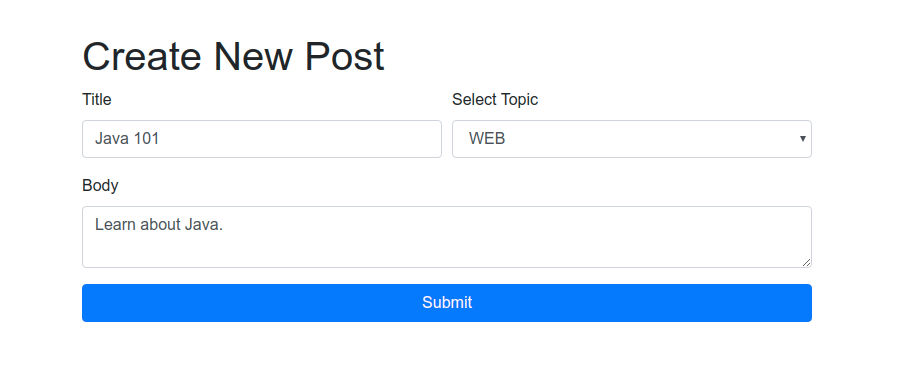
How to compare enum constants
You can easily compare enum constants using Thymeleaf conditionals to control what you want to display to the visitor.
Using the th:if attribute
The following example demonstrates how you can use the Thymeleaf th:if conditional attribute to conditionally display a text:
<th:block th:each="topic : ${T(com.attacomsian.runner.domains.constants.Topic).values()}">
<div th:if="${topic eq T(com.attacomsian.runner.domains.constants.Topic).WEB}">
Hey, I am a web developer!
</div>
</th:block>
Alternatively, you can also use string literal for comparison, as shown below:
<th:block th:each="topic : ${T(com.attacomsian.runner.domains.constants.Topic).values()}">
<div th:if="${topic.name() eq 'WEB'}">
Hey, I am a web developer!
</div>
</th:block>
Using the th:switch attribute
Another way to compare enum constants in Thymeleaf is by using the th:switch attribute, as shown below:
<div th:each="topic : ${T(com.attacomsian.runner.domains.constants.Topic).values()}">
<span th:text="${topic}"></span>
<th:block th:switch="${topic}" th:with="Topic=${T(com.attacomsian.runner.domains.constants.Topic)}">
<span th:case="${Topic.TECH}">- Technology Tutorials</span>
<span th:case="${Topic.DESIGN}">- Design Tutorials</span>
<span th:case="${Topic.WEB}">- Web Development Tutorials</span>
<span th:case="${Topic.STARTUP}">- Startups Tutorials</span>
<span th:case="${Topic.DEVTOOLS}">- Development Tools Tutorials</span>
</th:block>
</div>
Notice the local variable Topic we have declared above. So instead of writing the T() expression for every case, we only defined it once and then used the local variable everywhere.
Conclusion
That's all. In this article, we have learned how to use Java enum constants in Thymeleaf to render a drop-down list and compare them using conditionals to display additional texts.
Read Next: How to use Thymeleaf in Spring Boot
✌️ Like this article? Follow me on Twitter and LinkedIn. You can also subscribe to RSS Feed.